Materi Himpunan dalam Matematika Diskrit

Berita Terkait

Materi himpunan matematika diskrit – Materi himpunan dalam matematika diskrit merupakan fondasi penting dalam memahami berbagai konsep di bidang ilmu komputer dan matematika. Topik ini akan membahas definisi, operasi, relasi, dan berbagai aspek penting lainnya dari himpunan, yang akan membantu kita memahami struktur data dan algoritma dengan lebih baik.

Kita akan mulai dengan definisi dan konsep dasar himpunan, seperti himpunan kosong, himpunan tunggal, dan himpunan bagian. Kemudian, kita akan mempelajari operasi-operasi himpunan seperti gabungan, irisan, dan komplemen, disertai diagram Venn untuk visualisasi yang lebih mudah. Tak ketinggalan, kita juga akan membahas relasi dan fungsi, serta konsep himpunan kuasa dan kardinalitas. Pada akhirnya, kita akan mengaplikasikan prinsip inklusi-eksklusi dan melihat contoh soal serta penerapannya dalam ilmu komputer.

Definisi dan Konsep Dasar Himpunan

Himpunan merupakan konsep dasar dalam matematika diskrit yang digunakan untuk mengelompokkan objek-objek dengan sifat tertentu. Pemahaman tentang himpunan dan berbagai jenisnya sangat penting untuk mempelajari berbagai topik dalam matematika diskrit, seperti kombinatorika, teori graf, dan logika.

Definisi Himpunan

Dalam matematika diskrit, himpunan didefinisikan sebagai kumpulan objek yang terdefinisi dengan baik. Objek-objek dalam himpunan disebut anggota atau elemen himpunan. Keanggotaan suatu objek dalam himpunan dapat ditentukan dengan jelas.

Jenis-Jenis Himpunan

Terdapat beberapa jenis himpunan yang perlu dipahami. Berikut penjelasannya:

Himpunan Kosong: Himpunan yang tidak memiliki anggota. Dinotasikan dengan ∅ atau .
Himpunan Tunggal: Himpunan yang hanya memiliki satu anggota.
Himpunan Bagian: Suatu himpunan A adalah himpunan bagian dari himpunan B jika semua elemen A juga merupakan elemen B. Dinotasikan dengan A ⊂ B.
Himpunan Semesta: Himpunan yang memuat semua objek yang dipertimbangkan dalam suatu konteks tertentu. Biasanya dinotasikan dengan U.

Perbandingan Jenis-Jenis Himpunan

Berikut tabel yang membandingkan dan mengkontraskan jenis-jenis himpunan di atas:

Jenis Himpunan	Definisi	Contoh
Himpunan Kosong	Tidak memiliki anggota	Himpunan bilangan prima yang genap
Himpunan Tunggal	Hanya memiliki satu anggota	Himpunan huruf vokal pertama dalam alfabet
Himpunan Bagian	Semua elemen himpunan A juga merupakan elemen himpunan B	Jika A = 1, 2 dan B = 1, 2, 3, maka A adalah himpunan bagian dari B (A ⊂ B)
Himpunan Semesta	Meliputi semua objek yang dipertimbangkan dalam suatu konteks	Jika kita membahas bilangan bulat, himpunan semestanya bisa berupa semua bilangan bulat

Notasi dan Simbol dalam Teori Himpunan

Berikut notasi dan simbol yang umum digunakan dalam teori himpunan:

∈ : Merupakan anggota dari
∉ : Bukan anggota dari
⊂ : Himpunan bagian
⊃ : Mengandung
∪ : Gabungan
∩ : Irisan
– : Selisih
∅ atau : Himpunan kosong

Contoh Himpunan dalam Konteks Matematika Diskrit

Berikut beberapa contoh himpunan dalam konteks matematika diskrit:

Himpunan semua bilangan bulat positif: 1, 2, 3, …
Himpunan semua titik pada bidang koordinat.
Himpunan semua graf sederhana dengan 5 simpul.
Himpunan semua algoritma pencarian pada suatu struktur data.

Operasi Himpunan

Operasi himpunan merupakan cara untuk menggabungkan atau memanipulasi himpunan. Pemahaman terhadap operasi ini sangat penting dalam matematika diskrit karena memungkinkan kita untuk menganalisis dan memecahkan masalah yang melibatkan kumpulan objek.

Penjelasan Operasi Himpunan

Berikut ini adalah penjelasan mengenai operasi-operasi himpunan yang umum digunakan dalam matematika diskrit, beserta contoh-contohnya.

Gabungan (Union): Gabungan dari dua himpunan, A dan B, adalah himpunan yang berisi semua elemen yang ada di A atau di B (atau di keduanya). Disimbolkan dengan A ∪ B.
Irisan (Intersection): Irisan dari dua himpunan, A dan B, adalah himpunan yang berisi semua elemen yang ada di A dan di B. Disimbolkan dengan A ∩ B.
Komplemen (Complement): Komplemen dari suatu himpunan A, terhadap suatu himpunan semesta S, adalah himpunan yang berisi semua elemen di S yang bukan anggota A. Disimbolkan dengan A^c atau A’.
Selisih (Difference): Selisih dari himpunan A dan B, dinotasikan sebagai A – B, adalah himpunan yang berisi semua elemen di A yang bukan anggota di B.

Diagram Venn, Materi himpunan matematika diskrit

Diagram Venn digunakan untuk menggambarkan hubungan antar himpunan. Setiap himpunan digambarkan sebagai lingkaran atau area. Irisan, gabungan, dan komplemen dapat divisualisasikan dengan jelas menggunakan diagram ini.

Gabungan (Union): Bagian yang diarsir pada diagram Venn menunjukkan gabungan A dan B, meliputi semua anggota yang ada di A atau di B atau di keduanya.
Irisan (Intersection): Bagian yang diarsir pada diagram Venn menunjukkan irisan A dan B, meliputi semua anggota yang ada di A dan di B.
Komplemen (Complement): Bagian yang diarsir pada diagram Venn menunjukkan komplemen A terhadap himpunan semesta, meliputi semua anggota yang tidak ada di A.
Selisih (Difference): Bagian yang diarsir pada diagram Venn menunjukkan selisih A dan B, meliputi semua anggota yang ada di A tetapi tidak ada di B.

Contoh Soal

Berikut contoh penerapan operasi himpunan dalam soal matematika diskrit:

Misalkan A = 1, 2, 3, 4 dan B = 3, 4, 5, 6. Tentukan A ∪ B, A ∩ B, A – B, dan A ^c jika S = 1, 2, 3, 4, 5, 6, 7,
8.
Jawaban:

A ∪ B = 1, 2, 3, 4, 5, 6

A ∩ B = 3, 4

A – B = 1, 2

A ^c = 5, 6, 7, 8

Tabel Operasi Himpunan

Himpunan A	Himpunan B	A ∪ B	A ∩ B	A – B
1, 2	2, 3	1, 2, 3	2	1
a, b, c	c, d, e	a, b, c, d, e	c	a, b
	1, 2	1, 2

Penerapan dalam Kehidupan Sehari-hari

Operasi himpunan dapat diaplikasikan dalam berbagai aspek kehidupan sehari-hari, seperti dalam pengklasifikasian data, analisis statistik, dan logika.

Contohnya, dalam sebuah toko, himpunan pelanggan yang membeli produk A dan produk B dapat dihitung menggunakan operasi irisan.
Sebagai contoh lainnya, dalam sebuah sekolah, himpunan siswa yang mengambil mata pelajaran matematika dan fisika dapat dihitung dengan operasi irisan.

Relasi dan Fungsi

Relasi dan fungsi merupakan konsep penting dalam matematika diskrit yang menggambarkan hubungan antara elemen-elemen dalam himpunan. Pemahaman tentang relasi dan fungsi akan sangat membantu dalam mempelajari topik-topik lanjutan dalam matematika diskrit.

Jenis-Jenis Relasi

Relasi dalam matematika diskrit menggambarkan hubungan antara elemen-elemen dalam suatu himpunan. Beberapa jenis relasi penting meliputi:

Relasi Refleksif: Suatu relasi R pada himpunan A disebut refleksif jika untuk setiap elemen a ∈ A, ( a, a) ∈ R. Artinya, setiap elemen dalam himpunan tersebut berelasi dengan dirinya sendiri.
Relasi Simetris: Suatu relasi R pada himpunan A disebut simetris jika untuk setiap a, b ∈ A, jika ( a, b) ∈ R, maka ( b, a) ∈ R. Artinya, jika a berelasi dengan b, maka b juga berelasi dengan a.
Relasi Transitif: Suatu relasi R pada himpunan A disebut transitif jika untuk setiap a, b, c ∈ A, jika ( a, b) ∈ R dan ( b, c) ∈ R, maka ( a, c) ∈ R. Artinya, jika a berelasi dengan b dan b berelasi dengan c, maka a juga berelasi dengan c.

Contoh Relasi dan Fungsi

Berikut beberapa contoh relasi dan fungsi dalam matematika diskrit:

Relasi “lebih kecil dari atau sama dengan” pada himpunan bilangan bulat. Relasi ini refleksif, antisimetris, dan transitif. Contoh: (2, 2) ∈ R, (2, 5) ∈ R, (5, 8) ∈ R, (2, 8) ∈ R.
Relasi “habis dibagi” pada himpunan bilangan bulat positif. Contoh: (6, 3) ∈ R, (3, 1) ∈ R, (6, 1) ∈ R. Relasi ini transitif, namun bukan refleksif dan simetris.

Contoh Relasi dan Fungsi dalam Tabel

Berikut tabel yang menunjukkan beberapa contoh relasi dan fungsi:

Relasi	Himpunan	Penjelasan
x habis dibagi y	Bilangan bulat positif	Relasi transitif, bukan refleksif, dan bukan simetris.
x adalah ibu dari y	Himpunan manusia	Relasi bukan refleksif, bukan simetris, dan bukan transitif.
x dan y memiliki usia yang sama	Himpunan manusia	Relasi simetris, refleksif, dan transitif.

Menentukan Domain dan Range Fungsi

Domain suatu fungsi adalah himpunan semua nilai input yang mungkin, sedangkan range adalah himpunan semua nilai output yang mungkin. Cara menentukan domain dan range suatu fungsi tergantung pada bentuk fungsi tersebut. Misalnya, untuk fungsi yang dinyatakan dengan rumus, domain ditentukan dengan nilai yang tidak menyebabkan pembagian dengan nol atau akar dari bilangan negatif.

Contoh: Fungsi f(x) = 1/x memiliki domain semua bilangan real kecuali nol. Range-nya juga semua bilangan real kecuali nol.

Himpunan Kuasa

Himpunan kuasa (power set) dari suatu himpunan adalah himpunan yang berisi semua himpunan bagian dari himpunan tersebut. Konsep ini penting dalam matematika diskrit, khususnya dalam pemodelan dan analisis masalah kombinatorial.

Konsep Himpunan Kuasa

Himpunan kuasa dari suatu himpunan A, dinotasikan sebagai P(A), merupakan himpunan yang anggotanya adalah semua himpunan bagian dari A. Hal ini berarti setiap elemen dalam P(A) adalah suatu himpunan yang anggotanya merupakan subset dari A. Himpunan kosong juga merupakan subset dari setiap himpunan, sehingga selalu termasuk dalam himpunan kuasa.

Contoh Himpunan Kuasa

Jika A = 1, 2, maka P(A) = , 1, 2, 1, 2. Kardinalitas P(A) adalah 2 ² = 4.
Jika B = a, b, c, maka P(B) = , a, b, c, a, b, a, c, b, c, a, b, c. Kardinalitas P(B) adalah 2 ³ = 8.
Jika C = , maka P(C) = . Kardinalitas P(C) adalah 2 ⁰ = 1.

Hubungan Kardinalitas

Terdapat hubungan yang signifikan antara kardinalitas (banyaknya elemen) suatu himpunan dengan kardinalitas himpunan kuasanya. Jika |A| menyatakan kardinalitas himpunan A, maka kardinalitas himpunan kuasanya, |P(A)|, selalu sama dengan 2 ^|A|. Ini berarti jika suatu himpunan memiliki n elemen, maka himpunan kuasanya akan memiliki 2 ⁿ elemen.

Penerapan dalam Algoritma/Pemrograman

Konsep himpunan kuasa sering digunakan dalam algoritma dan pemrograman, terutama dalam pemodelan masalah kombinatorial. Misalnya, dalam algoritma pencarian solusi optimal, himpunan kuasa dapat digunakan untuk mengeksplorasi semua kemungkinan kombinasi atau subset dari suatu himpunan data. Contohnya dalam masalah pemilihan fitur pada machine learning, algoritma dapat menggunakan himpunan kuasa untuk mencoba semua kemungkinan kombinasi fitur yang dapat digunakan untuk pelatihan model.

Diagram Himpunan Kuasa

Diagram untuk menggambarkan himpunan kuasa dapat berupa diagram pohon atau tabel. Sebagai ilustrasi, jika himpunan A = a, b, maka himpunan kuasanya P(A) = , a, b, a, b. Diagram pohon akan menunjukkan setiap kemungkinan subset dari A, sedangkan tabel akan menampilkan semua subset dalam bentuk himpunan.

Himpunan A	Himpunan Kuasa P(A)
a, b	, a, b, a, b

Kardinalitas Himpunan

Kardinalitas himpunan mengacu pada ukuran atau jumlah elemen yang dikandungnya. Pemahaman tentang kardinalitas penting untuk mengklasifikasikan himpunan, baik yang berhingga maupun tak hingga, dan untuk memahami hubungan antara himpunan dalam konteks operasi himpunan.

Konsep Kardinalitas

Kardinalitas himpunan, dilambangkan dengan |A|, menunjukkan jumlah elemen yang ada dalam himpunan A. Untuk himpunan berhingga, kardinalitasnya merupakan bilangan bulat positif yang merepresentasikan jumlah anggota dalam himpunan tersebut. Untuk himpunan tak hingga, kardinalitasnya dapat dibedakan berdasarkan jenis tak hingganya.

Contoh Perhitungan Kardinalitas

Berikut beberapa contoh perhitungan kardinalitas untuk berbagai jenis himpunan:

Himpunan Berhingga: Misal himpunan A = 1, 2, 3, 4, 5. Kardinalitas himpunan A adalah |A| = 5.
Himpunan Kosong: Himpunan kosong, dilambangkan dengan Ø, memiliki kardinalitas |Ø| = 0.
Himpunan dengan Elemen yang Sama: Misal himpunan B = a, a, a, a. Walaupun terdapat pengulangan, kardinalitas himpunan B tetap |B| = 1 karena hanya ada satu elemen unik, yaitu ‘a’.

Hubungan dengan Operasi Himpunan

Kardinalitas dapat dikaitkan dengan operasi himpunan. Misalnya, kardinalitas gabungan dua himpunan A dan B dapat dihitung dengan rumus |A ∪ B| = |A| + |B|
-|A ∩ B|. Rumus ini mempertimbangkan bahwa elemen yang ada di perpotongan keduanya dihitung dua kali pada penjumlahan |A| dan |B|, sehingga perlu dikurangi satu kali.

Kardinalitas Himpunan Tak Hingga

Untuk himpunan tak hingga, konsep kardinalitas lebih kompleks. Himpunan bilangan bulat (Z) dan bilangan real (R) merupakan contoh himpunan tak hingga. Meskipun keduanya tak hingga, kardinalitasnya berbeda. Himpunan bilangan bulat memiliki kardinalitas yang sama dengan himpunan bilangan asli (N), yang dilambangkan sebagai |N| = א ₀ (aleph-nol). Sedangkan himpunan bilangan real memiliki kardinalitas yang lebih besar, yang dilambangkan sebagai |R| = c (kontinum).

Kardinalitas himpunan bilangan asli (N) sama dengan himpunan bilangan bulat (Z).

Perbedaan Himpunan Berhingga dan Tak Hingga

Perbedaan mendasar antara himpunan berhingga dan tak hingga terletak pada keterbatasan elemennya. Himpunan berhingga memiliki jumlah elemen yang terbatas dan dapat dihitung, sedangkan himpunan tak hingga memiliki jumlah elemen yang tak terbatas dan tidak dapat dihitung.

Himpunan Berhingga: Jumlah elemen dapat dihitung dengan cara menghitung satu per satu.
Himpunan Tak Hingga: Jumlah elemen tidak dapat dihitung karena selalu ada elemen baru yang dapat ditambahkan.

Prinsip Inklusi-Eksklusi

Materi, contoh soal Himpunan matematika diskrit.pptx

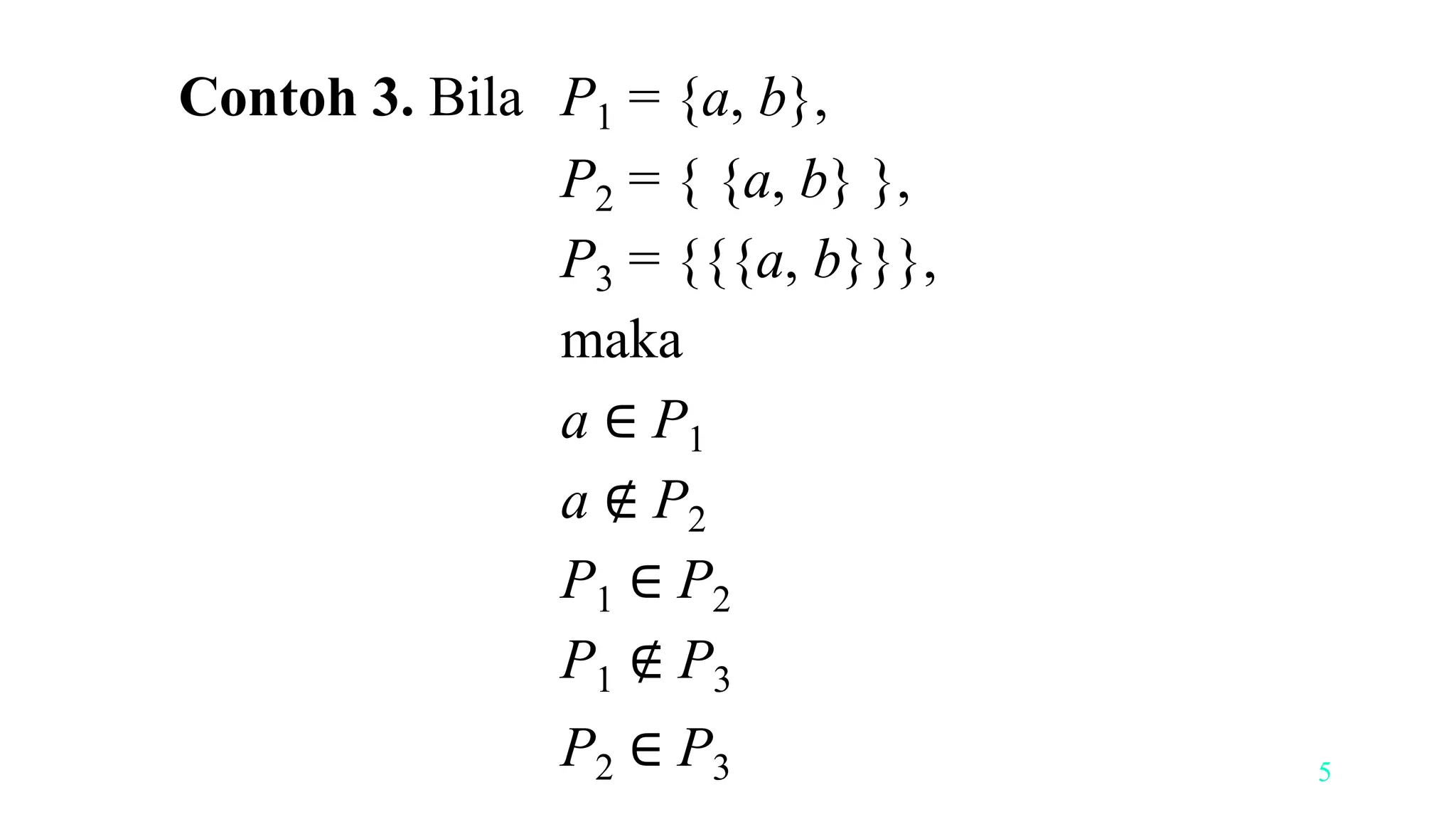
Prinsip inklusi-eksklusi merupakan teknik penting dalam kombinatorika untuk menghitung kardinalitas (ukuran) dari gabungan beberapa himpunan. Prinsip ini memungkinkan kita untuk menghitung jumlah elemen dalam gabungan himpunan tanpa harus menghitung setiap elemen secara terpisah.

Penjelasan Prinsip Inklusi-Eksklusi

Prinsip ini didasarkan pada gagasan bahwa jika kita menghitung kardinalitas gabungan dari beberapa himpunan, kita perlu berhati-hati untuk tidak menghitung elemen yang sama lebih dari sekali. Dengan prinsip inklusi-eksklusi, kita dapat menghindari penghitungan ganda ini.

Contoh Penerapan

Bayangkan kita ingin menghitung jumlah siswa di sebuah kelas yang menyukai matematika atau fisika. Misalnya, terdapat 30 siswa yang menyukai matematika, 25 siswa yang menyukai fisika, dan 10 siswa yang menyukai keduanya. Dengan prinsip inklusi-eksklusi, kita dapat menghitung jumlah siswa yang menyukai setidaknya satu mata pelajaran tersebut:

Siswa yang menyukai matematika: 30
Siswa yang menyukai fisika: 25
Siswa yang menyukai keduanya: 10

Jumlah siswa yang menyukai setidaknya satu mata pelajaran adalah 30 + 25 – 10 = 45.

Ilustrasi Visual

Prinsip inklusi-eksklusi dapat diilustrasikan dengan diagram Venn. Bayangkan dua himpunan, A dan B. Elemen yang berada di dalam lingkaran A mewakili siswa yang menyukai matematika, dan elemen di dalam lingkaran B mewakili siswa yang menyukai fisika. Daerah yang tumpang tindih antara kedua lingkaran mewakili siswa yang menyukai keduanya. Prinsip inklusi-eksklusi memungkinkan kita untuk menghitung total elemen di dalam gabungan A dan B dengan menghitung elemen di dalam A, elemen di dalam B, dan mengurangi elemen di dalam irisan A dan B.

Rumus Umum

|A ∪ B| = |A| + |B|
-|A ∩ B|

Rumus ini dapat digeneralisasikan untuk lebih dari dua himpunan. Misalnya, untuk tiga himpunan A, B, dan C:

|A ∪ B ∪ C| = |A| + |B| + |C|
-|A ∩ B|
-|A ∩ C|
-|B ∩ C| + |A ∩ B ∩ C|

Rumus umum untuk n himpunan dapat dirumuskan dengan menggunakan prinsip inklusi-eksklusi.

Contoh Soal dan Aplikasi

Materi himpunan memiliki beragam aplikasi dalam matematika diskrit, khususnya dalam ilmu komputer. Contoh penerapannya dapat ditemukan dalam algoritma, desain database, dan analisis data. Pemahaman tentang himpunan sangat penting untuk membangun fondasi dalam pemrograman dan pemecahan masalah dalam ilmu komputer.

Contoh Soal Matematika Diskrit

Berikut beberapa contoh soal matematika diskrit yang melibatkan konsep himpunan:

Soal: Diberikan himpunan A = 1, 2, 3, 4 dan himpunan B = 3, 4, 5, 6. Tentukan A ∪ B dan A ∩ B.
Solusi: A ∪ B adalah gabungan dari himpunan A dan B, yang berisi semua elemen yang ada di A atau B atau keduanya. A ∪ B = 1, 2, 3, 4, 5, 6. A ∩ B adalah irisan dari himpunan A dan B, yang berisi semua elemen yang ada di A dan B. A ∩ B = 3, 4.
Soal: Jika terdapat himpunan mahasiswa yang menyukai mata kuliah Algoritma (Himpunan A) dan himpunan mahasiswa yang menyukai mata kuliah Struktur Data (Himpunan B). Jika |A| = 25, |B| = 18, dan |A ∩ B| = 12, berapa jumlah mahasiswa yang hanya menyukai salah satu mata kuliah tersebut?
Solusi: Jumlah mahasiswa yang menyukai salah satu mata kuliah adalah |A ∪ B|. Dengan rumus |A ∪ B| = |A| + |B||A ∩ B|, maka |A ∪ B| = 25 + 18 – 12 = 31. Jadi, jumlah mahasiswa yang hanya menyukai salah satu mata kuliah adalah 31.

Penerapan dalam Ilmu Komputer

Konsep himpunan sangat penting dalam berbagai bidang ilmu komputer. Berikut beberapa contoh penerapannya:

Basis Data: Himpunan digunakan untuk merepresentasikan kumpulan data dalam database, seperti tabel dan relasi antar tabel. Operasi himpunan (seperti gabungan, irisan, dan selisih) digunakan untuk mengelola dan memanipulasi data dalam database.
Algoritma Pencarian: Beberapa algoritma pencarian, seperti pencarian Breadth-First Search (BFS) dan Depth-First Search (DFS), memanfaatkan struktur data berbasis himpunan untuk melacak simpul yang telah dikunjungi dan menghindari pengulangan.
Pengelolaan Sumber Daya: Dalam sistem operasi, himpunan digunakan untuk mengelola dan mengendalikan sumber daya sistem, seperti proses, memori, dan file.

Aplikasi dalam Algoritma

Himpunan digunakan dalam berbagai algoritma untuk mengelola dan memanipulasi data. Misalnya, algoritma untuk menentukan jalur terpendek atau permasalahan graf, seringkali menggunakan himpunan untuk merepresentasikan simpul, edge, dan jalur yang mungkin.

Contoh Kasus: Pertimbangkan algoritma untuk menemukan semua jalur terpendek antara dua simpul dalam sebuah graf. Algoritma tersebut dapat menggunakan himpunan untuk melacak simpul yang telah dikunjungi dan jalur yang telah ditemukan. Data yang disimpan dalam himpunan akan membantu menentukan jalur mana yang optimal.

Relevansi dalam Studi Kasus Kehidupan Nyata

Penerapan himpunan dalam kehidupan nyata sangat luas, terutama dalam pengelolaan data dan analisis. Berikut beberapa contohnya:

Manajemen Pelanggan: Perusahaan dapat menggunakan himpunan untuk mengklasifikasikan pelanggan berdasarkan preferensi pembelian, lokasi, atau karakteristik lainnya. Dengan menggunakan himpunan, perusahaan dapat membuat kampanye pemasaran yang lebih efektif dan personal.
Sistem Manajemen Perpustakaan: Perpustakaan dapat menggunakan himpunan untuk mengelola koleksi buku, mengklasifikasikan buku berdasarkan genre, dan menemukan buku yang sesuai dengan permintaan pengguna. Penggunaan himpunan dapat membantu perpustakaan mengelola koleksi dengan lebih terstruktur dan efisien.

Penutup: Materi Himpunan Matematika Diskrit

Materi himpunan matematika diskrit, meskipun terkesan mendasar, memiliki peran krusial dalam banyak bidang ilmu. Pemahaman yang baik tentang konsep-konsep di dalamnya akan sangat membantu dalam memecahkan masalah-masalah kombinatorik dan memahami struktur data dalam ilmu komputer. Semoga penjelasan ini memberikan gambaran yang komprehensif dan bermanfaat untuk Anda.